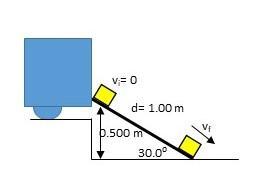
A 3.00-kg crate slides down a ramp. the ramp is 1.00 m in length and inclined at an angle of 30.08 as shown in the figure. The crate starts from rest at the top, experiences a constant friction force of magnitude 5.00 N, and continues to move a short distance on the horizontal floor after it leaves the ramp.
Answers
Answer:
2.55 m/s
Explanation:
A 3.00-kg crate slides down a ramp. the ramp is 1.00 m in length and inclined at an angle of 30° as shown in the figure. The crate starts from rest at the top, experiences a constant friction force of magnitude 5.00 N, and continues to move a short distance on the horizontal floor after it leaves the ramp. Use energy methods to determine the speed of the crate at the bottom of the ramp.
Solution:
The work done by friction is given as:
[tex]W_f=F_f\Delta S\\\\Where\ F_f\ is\ the \ frictional\ force=-5N(the\ negative \ sign\ because\ it\\acts\ opposite\ to \ direction\ of\ motion),\Delta S=slope\ length=1\ m\\\\W_f=F_f\Delta S=-5\ N*1\ m=-5J[/tex]
The work done by gravity is:
[tex]W_g=F_g*s*cos(\theta)\\\\F_g=force\ due\ to\ gravity=mass*acceleration\ due\ to\ gravity=3\ kg*9.81\\m/s^2, s=1\ m, \theta=angle\ between\ force\ and\ displacement=90-30=60^o\\\\W_g=3\ kg*9.81\ m/s^2*1\ m*cos(60)=14.72\ J\\\\The\ Kinetic\ energy(KE)=W_f+W_g=14.72\ J-5\ J=9.72\ J\\\\Also, KE=\frac{1}{2} mv^2\\\\9.72=\frac{1}{2} (3)v^2\\\\v=\sqrt{\frac{2*9.72}{3} } =2.55\ m/s[/tex]
Related Questions
Wind is caused by ___. the earth's tilt the Coriolis effect temperature differences humidity
Answers
I am guessing wind is caused by climate change in the atmosphere
Explanation:
wind is cause by climate change in the atmosphere that depends weather is is breezy really cold or rain and cold
Answer:
caused by the uneven heating of the Earth by the sun and the own rotation.
A 5.0-kg mass is placed at (3.0, 4.0) m, and a 6.0-kg mass is placed at (3.0, -4.0) m. What is the moment of inertia of this system of masses about the y-axis?
Answers
Answer:
the moment of inertia of this system of masses about the y-axis is 99 kgm²
Explanation:
Given the data in the question;
mass m₁ = 5.0 kg at point ( 3.0, 4.0 )
mass m₂ = 6.0 kg at point ( 3.0, -4.0 )
Now, Moment of inertia [tex]I[/tex] of this system of masses about the y-axis will be;
Moment of inertia [tex]I[/tex]ₓ = mixi²
Moment of inertia [tex]I[/tex] = m₁x₁² + m₂x₂²
we substitute
Moment of inertia [tex]I[/tex] = [ 5.0 × ( 3 )² ] + [ 6.0 × ( 3 )² ]
Moment of inertia [tex]I[/tex] = [ 5.0 × 9 ] + [ 6.0 × 9 ]
Moment of inertia [tex]I[/tex] = 45 + 54
Moment of inertia [tex]I[/tex] = 99 kgm²
Therefore, the moment of inertia of this system of masses about the y-axis is 99 kgm²
Determine the magnitude of the minimum acceleration at which the thief can descend using the rope. Express your answer to two significant figures and include the appropriate units.
Answers
Answer: hello your question is incomplete below is the missing part
A 69-kg petty thief wants to escape from a third-story jail window. Unfortunately, a makeshift rope made of sheets tied together can support a mass of only 58 kg.
answer:
To 2 significant Figures = 1.6 m/s^2
Explanation:
Calculate the magnitude of minimum acceleration at which the thief can descend
we apply the relation below
Mg - T = Ma --- ( 1 )
M = 69kg
g = 9.81
T = 58 * 9.81
a = ? ( magnitude of minimum acceleration)
From equation 1
a = [ ( 69 * 9.81 ) - ( 58 * 9.81 ) ] / 69
= 1.5639 m/s^2
To 2 significant Figures = 1.6 m/s^2
A police car in hot pursuit goes speeding past you. While the siren is approaching, the frequency of the sound you hear is 5500 Hz. When the siren is receding away from you, the frequency of the sound is 4500 Hz. Use the Doppler formula to determine the velocity of the police car. Use vsound=330 m/s.
What is the velocity v of the police car ?
Answers
I don’t have an explanation my apologies.
When a police car in hot pursuit goes speeding past you, the velocity v of the police car is 33 m/s.
What is the Doppler formula?The formula is used when there exists a Doppler shift. The Doppler shift is due to the relative motion of sound waves between the source and observer.
The frequency increase by the Doppler effect is represented by the formula
f' = [tex]\dfrac{v-v_{o} }{v-v_{s} }[/tex]× f
Given the frequency of source f' is 5500 Hz . Velocity of the observer v₀ is 0.
Substituting the value into the equation will give us the velocity of the police car.
[tex]5500 = \dfrac{330}{330-v} \times f[/tex]...........(1)
When the car is receding, the frequency of the receiving signal f = 4500 Hz.
[tex]4500 = \dfrac{330}{330+v} \times f[/tex]..........(2)
Solving both equation, we get the velocity of a police car.
v = 33 m/s
Therefore, the velocity v of the police car is 33 m/s.
Learn more about Doppler equation.
https://brainly.com/question/15318474
#SPJ2
Kulsum’s TV uses 45 W. How much does it cost her to watch TV for one month (30 days). She watches TV for 4 hours/day during mid-peak time (10.4 cents/kWh).
Answers
Answer:
Total cost = 56.16 cents
Explanation:
Given the following data;
Power = 45 Watts
Time = 4 hours
Number of days = 30 days
Cost = 10.4 cents
To find how much does it cost her to watch TV for one month;
First of all, we would determine the energy consumption of the TV;
Energy = power * time
Energy = 45 * 4
Energy = 180 Watt-hour = 180/1000 = 0.18 Kwh (1 Kilowatts is equal to 1000 watts).
Energy consumption = 0.18 Kwh
Next, we find the total cost;
Total cost = energy * number of days * cost
Total cost = 0.18 * 30 * 10.4
Total cost = 56.16 cents
An object with mass m = 0.56 kg is attached to a string of length r = 0.72 m and is rotating with an angular velocity ω = 1.155 rad/s. What is the centripetal force acting in the object?
Answers
Answer:
The centripetal force is 0.54 N.
Explanation:
mass, m = 0.56 kg
radius, r = 0.72 m
angular speed, w = 1.155 rad/s
The centripetal force is given by
[tex]F = m r w^2\\\\F =0.56\times 0.72\times 1.155\times 1.155\\\\F = 0.54 N[/tex]
help me with this question
Answers
Explanation:
Let's set the x-axis to be parallel to the and positive up the plane. Likewise, the y-axis will be positive upwards and perpendicular to the plane. As the problem stated, we are going to assume that m1 will move downwards so its acceleration is negative while m2 moves up so its acceleration is positive. There are two weight components pointing down the plane, [tex]m_1g \sin \theta[/tex] and [tex]m_2g \sin \theta[/tex] and two others pointing up the plane, the two tensions T along the strings. There is a normal force N pointing up from the plane and two pointing down, [tex]m_1g \sin \theta[/tex] and [tex]m_2g \sin \theta[/tex]. Now let's apply Newton's 2nd law to this problem:
x-axis:
[tex]m1:\:\:\:\displaystyle \sum_i F_i = T - m_1g \sin \theta = - m_1a\:\:\:\:(1)[/tex]
[tex]m2:\:\:\:\displaystyle \sum_i F_i = T - m_2g \sin \theta = m_2a\:\:\:\:(2)[/tex]
y-axis:
[tex]\:\:\:\displaystyle \sum_i F_i = N - m_1g \cos \theta - m_2g \cos \theta = 0[/tex]
Use Eqn 1 to solve for T,
[tex]T = m_1(g \sin \theta - a)[/tex]
Substitute this expression for T into Eqn 2,
[tex]m_1g \sin \theta - m_1a - m_2g \sin \theta = m_2a[/tex]
Collecting all similar terms, we get
[tex](m_1 + m_2)a = (m_1 - m_2)g \sin \theta[/tex]
or
[tex]a = \left(\dfrac{m_1 - m_2}{m_1 + m_2} \right)g \sin \theta[/tex]
why are you teachers regarded as professionals
Answers
Answer:
coz teaching is their profession.
1000 grams of water is heated from 0 degree to 200 degree . The specific heat of water is 4186 j/kg.°C. Estimate the change in entropy of the water.
Answers
Answer:2
Explanation:
A shooting star is actually the track of a meteor, typically a small chunk of debris from a comet that has entered the earth's atmosphere. As the drag force slows the meteor down, its kinetic energy is converted to thermal energy, leaving a glowing trail across the sky. A typical meteor has a surprisingly small mass, but what it lacks in size it makes up for in speed. Assume that a meteor has a mass of 1.5
Answers
Answer:
A. Power generated by meteor = 892857.14 Watts
Yes. It is obvious that the large amount of power generated accounts for the glowing trail of the meteor.
B. Workdone = 981000 J
Power required = 19620 Watts
Note: The question is incomplete. A similar complete question is given below:
A shooting star is actually the track of a meteor, typically a small chunk of debris from a comet that has entered the earth's atmosphere. As the drag force slows the meteor down, its kinetic energy is converted to thermal energy, leaving a glowing trail across the sky. A typical meteor has a surprisingly small mass, but what it lacks in size it makes up for in speed. Assume that a meteor has a mass of 1.5 g and is moving at an impressive 50 km/s, both typical values. What power is generated if the meteor slows down over a typical 2.1 s? Can you see how this tiny object can make a glowing trail that can be seen hundreds of kilometers away? 61. a. How much work does an elevator motor do to lift a 1000 kg elevator a height of 100 m at a constant speed? b. How much power must the motor supply to do this in 50 s at constant speed?
Explanation:
A. Power = workdone / time taken
Workdone = Kinetic energy of the meteor
Kinetic energy = mass × velocity² / 2
Mass of meteor = 1.5 g = 0.0015 kg;
Velocity of meteor = 50 km/s = 50000 m/s
Kinetic energy = 0.0015 × (50000)² / 2 = 1875000 J
Power generated = 1875000/2.1 = 892857.14 Watts
Yes. It is obvious that the large amount of power generated accounts for the glowing trail of the meteor.
B. Work done by elevator against gravity = mass × acceleration due to gravity × height
Work done = 1000 kg × 9.81 m/s² × 100 m
Workdone = 981000 J
Power required = workdone / time
Power = 981000 J / 50 s
Power required = 19620 Watts
Therefore, the motor must supply a power of 19620 Watts in order to lift a 1000 kg to a height of 100 m at a constant speed in 50 seconds.
A train starts from rest and accelerates uniformly until it has traveled 5.6 km and acquired a forward velocity of The train then moves at a constant velocity of for 420 s. The train then slows down uniformly at until it is brought to a halt. The acceleration during the first 5.6 km of travel is closest to which of the following?
a. 0.19 m/s^2
b. 0.14 m/s^2
c. 0.16 m/s^2
d. 0.20 m/s^2
e. 0.17 m/s^2
Answers
Answer:
The acceleration during the first 5.6 km of travel is closest to 0.16 m/s²
Option c) 0.16 m/s² is the correct answer.
Explanation:
Given the data in the question;
since the train starts from rest,
Initial velocity; u = 0 m/s
final velocity; v = 42 m/s
distance covered S = 5.6 km = ( 5.6 × 1000 )m = 5600 m
acceleration a = ?
From the third equation of motion;
v² = u² + 2as
we substitute in our values
( 42 )² = ( 0 )² + [ 2 × a × 5600 ]
1764 = 0 + [ 11200 × a ]
1764 = 11200 × a
a = 1764 / 11200
a = 0.1575 ≈ 0.16 m/s² { two decimal place }
Therefore, The acceleration during the first 5.6 km of travel is closest to 0.16 m/s²
Option c) 0.16 m/s² is the correct answer.
what is measured by the ammeter
Answers
Answer:
amperes
Ammeter, instrument for measuring either direct or alternating electric current, in amperes. An ammeter can measure a wide range of current values because at high values only a small portion of the current is directed through the meter mechanism; a shunt in parallel with the meter carries the major portion.
Explanation:
hope it helps
A pilot drops a package from a plane flying horizontally at a constant speed. Neglecting air resistance, when the package hits the ground the horizontal location of the plane will Group of answer choices be behind the package. be over the package. be in front of the package depend of the speed of the plane when the package was released.
Answers
Answer:
The location of helicopter is behind the packet.
Explanation:
As the packet also have same horizontal velocity as same as the helicopter, and also it has some vertical velocity as it hits the ground.
The horizontal velocity remains same as there is no force in the horizontal direction. The vertical velocity goes on increasing as acceleration due to gravity acts.
So, the helicopter is behind the packet.
Increasing the surfactant concentration above the critical micellar concentration
will result in: Select one:
1.An increase in surface tension
2. A decrease in surface tension
3. No change in surface tension
4.None of the above
Answers
Answer:
Explanation:no change in surface tension
An increase in the surfactant concentration above the critical micellar concentration will result in no change in surface tension.
In water-gas interface, surfactant reduces the surface tension of water by adsorbing at the liquid–gas interface.
Also, in oil-water interface, surfactant reduces the interfacial tension between oil and water by adsorbing at the oil-water interface.
The concentration of the surfactant can increase to a level called critical micellar concentration, which is an important characteristic of a surfactant.
As the concentration of the surfactant increases before critical micellar concentration, the surface tension changes strongly with an increase in the concentration of the surfactant. After reaching the critical micellar concentration, any further increase in the concentration will result in no change of the surface tension, that is the surface tension will be constant.Thus, increasing the surfactant concentration above the critical micellar concentration will result in no change in surface tension.
Learn more here: https://brainly.com/question/15785205
Human vision cuts off on the red side of the spectrum at about 675 nm. What is the energy of a photon (in J) of this wavelength?
Answers
Answer:
The energy of a photon is 2.94x10⁻¹⁹ J.
Explanation:
The energy of the photon is given by:
[tex] E = \frac{hc}{\lambda} [/tex]
Where:
h: is Planck's constant = 6.62x10⁻³⁴ J.s
c: is the speed of light = 3.00x10⁸ m/s
λ: is the wavelength = 675 nm
Hence, the energy is:
[tex] E = \frac{hc}{\lambda} = \frac{6.62 \ccdot 10^{-34} J.s*3.00 \cdot 10^{8} m/s}{675 \cdot 10^{-9} m} = 2.94 \cdot 10^{-19} J [/tex]
Therefore, the energy of a photon is 2.94x10⁻¹⁹ J.
I hope it helps you!
An 8.50 kg point mass and a 14.5 kg point mass are held in place 50.0 cm apart. A particle of mass (m) is released from a point between the two masses 12.0 cm from the 8.50 kg mass along the line connecting the two fixed masses.Find the magnitude of the acceleration of the particle.
Answers
Answer:
[tex]a=2.8*10^{-9}m/s[/tex]
Explanation:
From the question we are told that:
First Mass [tex]m=8.50kg[/tex]
2nd Mass [tex]m=14.5kg[/tex]
Distance
[tex]d_1=50=>0.50m\\\\d_2=>12cm=>0.12m[/tex]
Generally the Newtons equation for Gravitational force is mathematically given by
[tex]F_n=\frac{Gm_nm}{(r_n)^2}[/tex]
Therefore
Initial force on m
[tex]F_1=\frac{Gm_1m}{(r_1)^2}[/tex]
Final force on m
[tex]F_2=\frac{Gm_2m}{(r_2)^2}\\\\F=\frac{Gm_1m}{(r_1)^2}-\frac{Gm_2m}{(r_2)^2}[/tex]
Acceleration of m
[tex]a=\frac{F}{m}\\\\a=\frac{Gm_1}{r_1^2}-\frac{Gm_2}{r_2^2}[/tex]
[tex]a=6,67*10^{-11}{\frac{8.5}{0.12}}-\frac{14.5}{0.50}[/tex]
[tex]a=2.8*10^{-9}m/s[/tex]
LC-circuit of the radio receiver consists of variable capacitor (Cmin= 1 pF, Cmax=10 pF) and inductor
with inductance 1 µH. Determine the wavelength range of this radio receiver.
Answers
Answer:
the radio can tune wavelengths between 1.88 and 5.97 m
Explanation:
The signal that can be received is the one that is in resonance as the impedance of the LC circuit.
X = X_c - X_L
X = 1 / wC - w L
at the point of resonance the two impedance are equal so their sum is zero
X_c = X_L
1 / wC = w L
w² = 1 / CL
w = [tex]\sqrt{\frac{1}{CL} }[/tex]
let's look for the extreme values
C = 1 10⁻¹² F
w = [tex]\sqrt{\frac{1}{ 1 \ 10^{-12} \ 1 \ 10^{-6}} }[/tex]
w = [tex]\sqrt{1 \ 10^{18}}[/tex]
w = 10⁹ rad / s
C = 10 10⁻¹² F
w = [tex]\sqrt{\frac{1}{10 \ 10^{-12} \ 1 \ 10^{-6}} }[/tex]Ra 1/10 10-12 1 10-6
w = [tex]\sqrt{0.1 \ 10^{18}}[/tex]Ra 0.1 1018
w = 0.316 10⁹ rad / s
Now the angular velocity and the frequency are related
w = 2π f
f = w / 2π
the light velocity is
c = λ f
λ = c / f
we substitute
λ = c 2π/w
we calculate the two values
C = 1 pF
λ₁ = 3 10⁸ 2π / 10⁹
λ₁= 18.849 10⁻¹ m
λ₁ = 1.88 m
C = 10 pF
λ₂ = 3 10⁸ 2π / 0.316 10⁹
λ₂ = 59.65 10⁻¹ m
λ₂ = 5.97 m
so the radio can tune wavelengths between 1.88 and 5.97 m
Determine the tension in the string that connects M2 and M3.
Answers
☺️☺️☺️☺️☺️☺️☺️☺️☺️☺️✌️✌️✌️✌️✌️✌️✌️✌️❤️❤️❤️
Who stated that man is an animal
Answers
g you hang an object of mass m on a spring with spring constant k and find that it has a period of T. If you change the spring to one that has a spring constant of 2 k, the new period is
Answers
Answer:
a) T = 2π [tex]\sqrt{\frac{m}{k} }[/tex], b) T ’= [tex]\frac{1}{\sqrt{2} } T[/tex]
Explanation:
a) A system formed by a mass and a spring has a simple harmonic motion with angular velocity
w² = k / m
angular velocity and period are related
w = 2π /T
we substitute
4π²/ T² = k / m
T = 2π [tex]\sqrt{\frac{m}{k} }[/tex]
b) We change the spring for another with k ’= 2 k, let's find the period
T ’= 2π [tex]\sqrt{\frac{m}{k'} }[/tex]
T ’= 2π [tex]\sqrt{ \frac{m}{2k} }[/tex]
T ’= [tex]\frac{1}{\sqrt{2} } T[/tex]
A 1 500-kg car rounds an unbanked curve with a radius of 52 m at a speed of 12.0 m/s. What minimum coefficient of friction must exist between the road and tires to prevent the car from slipping
Answers
Explanation:
The centripetal force [tex]F_c[/tex] on the car must equal the frictional force f in order to avoid slipping off the road. Let's apply Newton's 2nd law to the y- and x-axes.
[tex]y:\:\:\:\:N - mg = 0[/tex]
[tex]x:\:\:F_c = f \Rightarrow \:\:\:m \dfrac{v^2}{r} = \mu N[/tex]
or
[tex]m \dfrac{v^2}{r} = \mu mg[/tex]
Solving for [tex]\mu[/tex],
[tex]\mu = \dfrac{v^2}{gr} = \dfrac{(12.0\:\frac{m}{s})^2}{(9.8\:\frac{m}{s^2})(52\:m)} = 0.28[/tex]
A 3 5m container is filled with 900 kg of granite (density of 2400 3 kg m/ ). The rest of the volume is air, with density equal to 3 1.15 / kg m . Find the mass of air and the overall (average) specific volume
Answers
Complete question:
A 5-m³ container is filled with 900 kg of granite (density of 2400 kg/m3). The rest of the volume is air, with density equal to 1.15 kg/m³. Find the mass of air and the overall (average) specific volume.
Answer:
The mass of the air is 5.32 kg
The specific volume is 5.52 x 10⁻³ m³/kg
Explanation:
Given;
total volume of the container, [tex]V_t[/tex] = 5 m³
mass of granite, [tex]m_g[/tex] = 900 kg
density of granite, [tex]\rho _g[/tex] = 2,400 kg/m³
density of air, [tex]\rho_a[/tex] = 1.15 kg/m³
The volume of the granite is calculated as;
[tex]V_g = \frac{m_g}{ \rho_g}\\\\V_g = \frac{900 \ kg}{2,400 \ kg/m^3} \\\\V_g = 0.375 \ m^3[/tex]
The volume of air is calculated as;
[tex]V_a = V_t - V_g\\\\V_a = 5 \ m^3 \ - \ 0.375 \ m\\\\V_a = 4.625 \ m^3[/tex]
The mass of the air is calculated as;
[tex]m_a = \rho_a \times V_a\\\\m_a = 1.15 \ kg/m^3 \ \times \ 4.625 \ m^3\\\\m_a = 5.32 \ kg[/tex]
The specific volume is calculated as;
[tex]V_{specific} = \frac{V_t}{m_g \ + \ m_a} = \frac{5 \ m^3}{900 \ kg \ + \ 5.32\ kg} = 5.52 \times 10^{-3} \ m^3/kg[/tex]
what change occurs to the mass of an object when a unbalanced
Answers
Answer:
The mass decreases
Explanation:
Just smart
Your car breaks down in the middle of nowhere. A tow truck weighing 4000 lbs. comes along and agrees to tow your car, which weighs 2000 lbs., to the nearest town. The driver of the truck attaches his cable to your car at an angle of 20 degrees to horizontal. He tells you that his cable has a strength of 500 lbs. He plans to take 10 secs to tow your car at a constant acceleration from rest in a straight line along a flat road until he reaches the maximum speed of 45 m.p.h. Can the driver carry out the plan
Answers
Answer:
F = 1010 Lb
the tension on the cable is greater than its resistance, which is why the plan is not viable
Explanation:
For this exercise we can use the kinematic relations to find the acceleration and with Newton's second law find the force to which the cable is subjected.
v = v₀ + a t
how the car comes out of rest v₀ = 0
a = v / t
let's reduce to the english system
v = 45 mph (5280 ft / 1 mile) (1h / 3600) = 66 ft / s
let's calculate
a = 66/10
a = 6.6 ft / s²
now let's write Newton's second law
X axis
Fₓ = ma
with trigonometry
cos 20 = Fₓ / F
Fₓ = F cos 20
we substitute
F cos 20 = m a
F = m a / cos20
W = mg
F = [tex]\frac{W}{g} \ \frac{a}{cos 20}[/tex]
let's calculate
F = [tex]\frac{2000}{32} \ \frac{6.6 }{cos20}[/tex](2000/32) 6.6 / cos 20
F = 1010 Lb
Under these conditions, the tension on the cable is greater than its resistance, which is why the plan is not viable.
ou charge a piece of aluminum foil (mass = 4.99 g) by touching it to a charged rod. The charged rod gives the aluminum foil a charge of 13 µC. Your professor brings a charged plate over and tells you to put the aluminum foil on top of the plate. To your surprise the aluminum foil hovers motionless in the air above it! Calculate the value of the electric field from the charged plate (assume it is a uniform field and the aluminum foil is a point charge).
Answers
Answer:
The appropriate answer is "3761.69 N/C".
Explanation:
Given that:
Mass,
m = 4.99 g
or,
= [tex]4.99\times 10^{-3} \ kg[/tex]
Charge,
q = 13 µC
or,
= [tex]13\times 10^{-6} \ C[/tex]
As we know,
⇒ [tex]F=mg=Eq[/tex]
then,
⇒ [tex]E=\frac{mg}{q}[/tex]
By putting the values, we get
[tex]=\frac{4.99\times 10^{-3}\times 9.8}{13\times 10^{-6}}[/tex]
[tex]=3761.69 \ N/C[/tex]
An irregular shape object has a mass of 19 oz. A graduated cylinder with and initial volume of 33.9 mL. After the object was dropped in the graduated cylinder, it had a volume of 92.8 mL. What is the density of object( g/mL)
Answers
Explanation:
m = 19 oz × (28.3 g/1 oz) = 537.7 g
V = 92.8 mL
[tex]\rho = \dfrac{m}{V}= \dfrac{537.7\:g}{92.8\:mL} = 5.79\:\frac{g}{mL}[/tex]
A 70-kg boy is surfing and catches a wave which gives him an initial speed of 1.6 m/s. He then drops through a height of 1.60 m, and ends with a speed of 8.5 m/s. How much nonconservative work (in kJ) was done on the boy
Answers
Answer:
3.6 KJ
Explanation: Given that a 70-kg boy is surfing and catches a wave which gives him an initial speed of 1.6 m/s. He then drops through a height of 1.60 m, and ends with a speed of 8.5 m/s. How much nonconservative work (in kJ) was done on the boy
The workdone = the energy.
There are two different energies in the scenario - the potential energy (P.E ) and the kinetic energy ( K.E )
P.E = mgh
P.E = 70 × 9.8 × 1.6
P.E = 1097.6 J
P.E = 1.098 KJ
K.E = 1/2mv^2
K.E = 1/2 × 70 × 8.5^2
K.E = 2528.75 J
K.E = 2.529 KJ
The non conservative workdone = K.E + P.E
Work done = 1.098 + 2.529
Work done = 3.63 KJ
Therefore, the non conservative workdone is 3.6 KJ approximately
plz answer the question
Answers
Answer:
Ray A - incident ray
Ray B - reflected ray
A child throws a ball vertically upward to a friend on a balcony 28 m above him. The friend misses the ball on its upward flight but catches it as it is falling back to earth. If the friend catches the ball 3.0 s after it is thrown, at what time did it pass him on its upward flight
Answers
Answer:
[tex]t=1.9 sec[/tex]
Explanation:
From the question we are told that:
Height [tex]h=28m[/tex]
Time [tex]t=3s[/tex]
Generally the Newton's equation for Initial velocity upward is mathematically given by
[tex]s=ut+\frtac{1}{2}at^2[/tex]
[tex]28=3u-\frac{1}{2}*9.8*3^2[/tex]
[tex]u=24.03m/s[/tex]
Generally the velocity at elevation and depression occurs as ball arrives and passes through S=28
[tex]v=\sqrt{24.03-2*9.8*28}[/tex]
[tex]v=5.35m/s and -5.35m/s[/tex]
Generally the Newton's equation for time to reach initial velocity is mathematically given by
[tex]v=u+at[/tex]
[tex]5.35=24.03-9.8t[/tex]
[tex]t=\frac{28.03-5.35}{9.8}[/tex]
[tex]t=1.9 sec[/tex]
A helicopter is ascending vertically witha speed of 5.40 m/s. At a height of 105 m above the earth a package is dropped from the helicopter. How much time does is take for the package to reach the ground
Answers
Answer: 5.21 s
Explanation:
Given
Helicopter ascends vertically with [tex]u=5.4\ m/s[/tex]
Height of helicopter [tex]h=105\ m[/tex]
When the package leaves the helicopter, it will have the same vertical velocity
Using equation of motion
[tex]\Rightarrow h=ut+\dfrac{1}{2}at^2\\\\\Rightarrow 105=-5.4t+0.5\times 9.8t^2\\\Rightarrow 4.9t^2-5.4t-105=0\\\\\Rightarrow t=\dfrac{5.4\pm \sqrt{5.4^2+4\times 4.9\times 105}}{2\times 4.9}\\\\\Rightarrow t=\dfrac{5.4\pm 45.68}{9.8}\\\\\Rightarrow t=5.21\ s\quad \text{Neglect negative value}[/tex]
So, package will take 5.21 s to reach the ground