Answers
Step-by-step explanation:
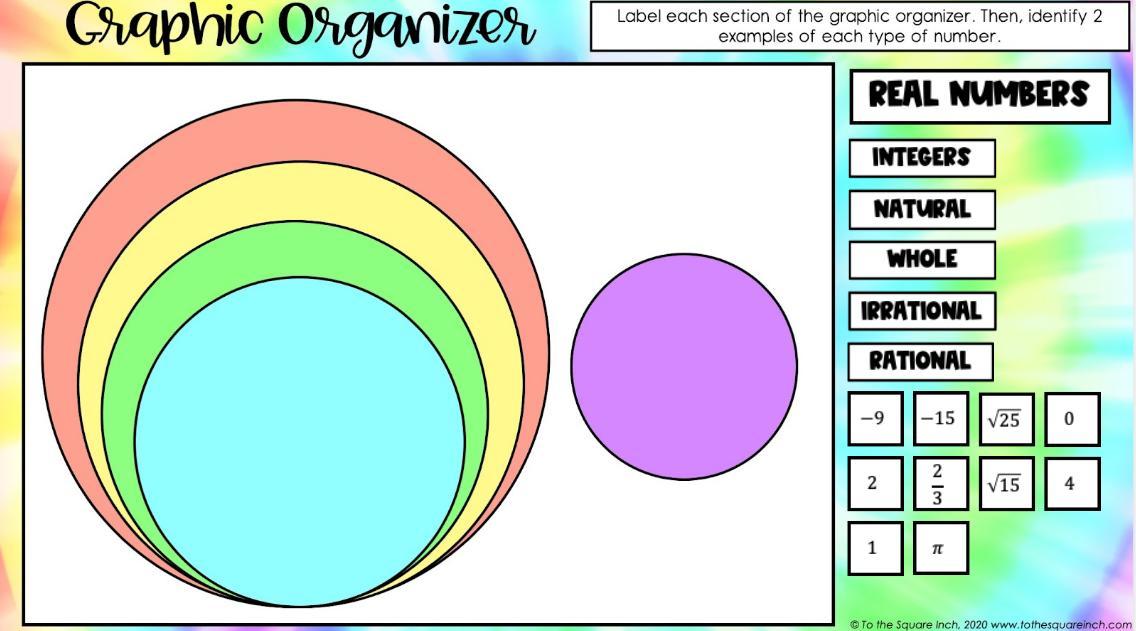
blue is natural: 1, 4, 0, 2 and root of 25.
green is whole: -9 and -15.
yellow is rational: 2/3
orange is irrational: pi and root of 15.
white is real numbers.
don't know about that purple one.
Related Questions
Julissa is printing out copies for a work training. It takes 4 minutes to print a color copy, and it takes 2 minutes to print a grayscale copy. She needs to print no fewer than 8 copies within 25 minutes.
Which system of inequalities represents the number of color copies, x, and grayscale copies, y, that Julissa can print to meet her goal?
Answers
Answer:
4x + 2y ≤ 25 , x + y ≥ 8 is the required system of inequalities to represent the given situation.
Step-by-step explanation:
Here, let the number of color copies = x
Now, the time taken to print each color copy = 4 minutes
⇒Time taken to print x color copies = x times ( Time taken by each copy)
= 4 (x) = 4x
and let the number gray scale copies = y
The time taken to print each gray scale copy = 2 minutes
⇒Time taken to print y gray scale copy = y times (Time taken by each copy)
= 2 (y) = 2y
Total copies printed = x + y
Maximum time taken to print x color copies and y grayscale copies
= 4x + 2y
So, according to the question:
4x + 2y ≤ 25 ( as maximum allotted time is 25 minutes)
and x + y ≥ 8 (as minimum number of copies is 8)
hence, the above system is the required system of inequalities to represent the given situation.
I hope this helps.
what is 4xy - 5y² - 3x² from 5x + 3y² - xy ?
Answers
[tex]▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪[/tex]
The equivalent expression is ~
[tex] \boxed{ \sf8 {y}^{2} + 3 {x}^{2} + 5x - 5xy}[/tex]
[tex] \large \boxed{ \mathfrak{Step\:\: By\:\:Step\:\:Explanation}}[/tex]
Let's solve ~
[tex]5x² + 3 {y}^{2} - xy - (4xy - 5y {}^{2} - 3 {x}^{2} )[/tex][tex]5x² + 3 {y}^{2} - xy - 4xy +5 {y}^{2} + 3 {x}^{2} [/tex][tex]3 {y}^{2} + 5 {y}^{2} + 3 {x}^{2} + 5x² - xy - 4xy[/tex][tex]8 {y}^{2} + 8 {x}^{2} - 5xy[/tex]solve |8y+4|=2|y-1|
please show the work!
Answers
8y+4 = 2y-2
8y-2y+4 = -2
6y+4 = -2
6y = -2-4
6y = -6
y = -1