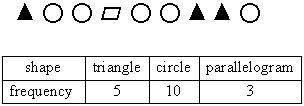
Chuck performed an experiment with a list of shapes. He randomly chose a shape from the list and recorded the results in the frequency table. The list of shapes and the frequency table are given below. Find the experimental probability of a parallelogram being chosen.

A scale of 1:5000000 means that:

This is mainly used in map or shadow etc. things.

For example in map it is given that the scale is 1mm:5000000mm, then it means that 1mm on the map is equal to 5000000mm in real life. So, you can be asked what does 5mm on map means in real life. So, you have to solve like this:

5 × 5000000 = real life size

25000000mm = real life size

In shadow like question, it can be asked that if 5000000 m of building casts a shadow of 1 m, then how much will be the shadow of a 10000000 m building. So, you have to solve it like this:

(10000000/5000000) × 1 = shadow size

=> 2 × 1 = shadow size

=> 2m = shadow size

You can tell me the specific questions so that I can help.

The scale 1:500 000 mean​s 1 unit on a map represents 500000 in real life

Scales are used to represent big or small measurements on a map or graph

The scale is given as:

1:500 000

The above means that:

1 unit on a map represents 500000 in real life

Read more about scale at:

https://brainly.com/question/3457976

#SPJ6

5 belong to whole number. b I don't know

Step-by-step explanation:

Assuming figure to be trapezoid,

Perimeter=6+4+7+4yd

=21 yd

Area of trapezoid=((6+7)/2) x ((4)^2-(0.5)^2)

=(13/2)x(16-0.25)

=6.5 x 15.75

=102.375 Sq yards

Answer:

true. true. false.

Step-by-step explanation: i’m in love with the shape of u. we push and pull like magnet whatever

Answer:

Non of these.

Step-by-step explanation:

Answer:

15 minutes

Step-by-step explanation:

Suly watched a film that was 90 minutes long. Then, she stopped at the [tex]\frac{1}{6}[/tex]mark. This means that we have to find [tex]\frac{1}{6}[/tex] of 90 minutes to find the amount of time Suly watched before the pizza man arrived. So therefore, the answer is 15 minutes.

Have a nice day. : )

Answer:

15 minutes

Step-by-step explanation:

Given:

Steps:

Answer:

A, c, d

Step-by-step explanation:

Answer:

C & D

Step-by-step explanation:

In order to find the perimeter, we would need to add all the sides. w+L+w+L would be adding the lengths and the widths. Simplifying this, we would get 2w, because there are 2 sides that are the same width, and 2 sides that are 2 lengths.

w+L+w+L or w+w+L+L or 2w+2L

Hope this helps!

--Applepi101

Step-by-step explanation:

53 is the correct answer

Answer:

The fourth (last) function is the correct one.

Step-by-step explanation:

Look at the parent function y = √x,  Its graph goes through (0, 0).  On the other hand, if y = √(x - h), the graph goes through (h, 0) if h is positive, and the graph is translated h units to the right from the graph of y = √x.  If h is negative, the graph is translated h units to the left.

In the four possible answers given, the values of h are {-4, 9, 5, -9}, in that order.  h = -9 results in the graph that is positioned 9 units to the left of the graph of y = √x.  This graph is furthest to the left.  Thus the fourth choice is the correct one.

Answer:

Option A

Step-by-step explanation:

From the graph attached,

Distance of point A of rectangle ABCD = 5 units

Distance of point E of rectangle EFGH = 5 units

Similarly, all the vertices of the rectangles ABCD and EFGH are equidistant from the y-axis.

Therefore, rectangle ABCD and rectangle EFGH may overlap each other by reflecting each other across y-axis.

Let's check by the rule of reflection,

Rule for the reflection of a point (x, y) across y-axis is given by,

(x, y) → (-x, y)

Following this rule,

A(-5, 5) → E(5, 5)

B(-3, 4) → F(3, 4)

C(-4, 1) → G(4, 1)

D(-6, 2) → H(6, 2)

Therefore, rule for the reflection is applicable in this question.

Option A will be the answer.

Answer:

[tex]n=1.3\times 10^{12}[/tex]

Step-by-step explanation:

Given that,

The radius of a cell, r = 10⁻³ cm

The density of the cell, d = 1.1 g/cm³

The weight of the Koala, m = 6 kg = 6000 grams

The density of an object is given by:

[tex]d=\dfrac{m}{V}[/tex]

For n cells,

[tex]nd=\dfrac{m}{V}\\\\n=\dfrac{m}{dV}[/tex]

Put all the values,

[tex]n=\frac{6000}{\frac{4}{3}\cdot\pi\cdot\left(10^{-3}\right)^{3}\cdot1.1}\\\\n=1.3\times 10^{12}[/tex]

So, there are [tex]1.3\times 10^{12}[/tex]cells in the average koala.

Answer:

There are 2,184 ways to select a first-place, second-place, and third-place winner.

The probability that all three winners are from Midland High is 0.0275.

The probability that all three winners are from Cassville High is 0.0549

Step-by-step explanation:

Since a local chess tournament gives medals for first, second, and third place, and there are five students from Midland High, three students from Leasburg High, and six students from Cassville High competing in the tournament, to determine which of the following statements are true, the following calculations must be performed:

A) There are 2,184 ways to select a first-place, second-place, and third-place winner.

5 + 3 + 6 = 14

14 x 13 x 12 = X

182 x 12 = X

2.184 = X

B) The probability that all three winners are from Midland High is 0.0275.

5/14 x 4/13 x 3/12 = X

0.02747 = X

C) The probability that all three winners are from Leasburg High is 0.0046.

3/14 x 2/13 x 1/12 = X

0.00274 = X

D) The probability that all three winners are from Cassville High is 0.0549

6/14 x 5/13 x 4/12 = X

0.0549 = X

Answer:

A, B, C, E

Step-by-step explanation:

Edg 2021

Branliest?

Answer:

3.4

Step-by-step explanation:

0.5x + 0.3=2

then I subtracted 0.3 from both sides which I got 1.7 then I divided by 0.5x and then I got 3.4

Answer:

x - y = 25

Step-by-step explanation:

3x - 4y = 15

-2x + 3y = 10

Add the two equations together

 3x - 4y = 15

-2x + 3y = 10

----------------------

x - y = 25

Answer:

[tex]{\Huge{\underline{\underline{\textbf{\textsf{Answer}}}}}}[/tex]

>> 3x - 4y = 15

>> -2x + 3y = 10

Add the two equations together

>> 3x - 4y = 15

>> -2x + 3y = 10

----------------------

Hence, x - y = 25

Answer:

5

Step-by-step explanation:

As for estimation, you may round 39.76 to the whole number, resulting in 40.

7.94 to 8

40 / 8 = 5

5 is your answer for the result of estimation

Answer:

A.)

Step-by-step explanation:

A.)

Answer:

A :)

Step-by-step explanation:

Answer:

[tex]\displaystyle \sec A=\frac{65}{63}[/tex]

Step-by-step explanation:

We are given that:

[tex]\displaystyle \csc A=\frac{65}{16}[/tex]

Where A is in QI.

And we want to find sec(A).

Recall that cosecant is the ratio of the hypotenuse to the opposite side. So, find the adjacent side using the Pythagorean Theorem:

[tex]a=\sqrt{65^2-16^2}=\sqrt{3969}=63[/tex]

So, with respect to A, our adjacent side is 63, our opposite side is 16, and our hypotenuse is 65.

Since A is in QI, all of our trigonometric ratios will be positive.

Secant is the ratio of the hypotenuse to the adjacent. Hence:

[tex]\displaystyle \sec A=\frac{65}{63}[/tex]

Answer:

Step-by-step explanation:

cosec A =60/16

hypotenuse/opposite = 60/16 =15/4 (in simplest form)

therefore hypotenuse = 15 , opposite = 4  

then adjacent =? (let be x)

using pythagoras theorem to find adjacent

opposite^2 + adjacent^2 = hypotenuse^2

4^2 + x^2 = 15^2

16 + x^2 = 225

x^2 = 225 - 16

x^2 = 209

[tex]x=\sqrt{209}[/tex]

sec A =hypotenuse/adjacent

[tex]=\frac{15}{\sqrt{209} }[/tex]

[tex]=\frac{15}{\sqrt{209} } * \frac{\sqrt{209} }{\sqrt{209} }[/tex]

=[tex]\frac{15\sqrt{209} }{209}[/tex]

Answer:

A. LHS,

3×(4+6)

3×10

30

NOW,

RHS,

(3×4)+(3×6)

12+18

30

Therefore, A is ans

Answer:

vertex = (- 4, - 75 )

Step-by-step explanation:

Given a quadratic in standard form

y = ax² + bx + c ( a ≠ 0 )

Then the x- coordinate of the vertex is

x = - [tex]\frac{b}{2a}[/tex]

y = 4x² + 32x - 11 ← is in standard form

with a = 4, b = 32 , then

x = - [tex]\frac{32}{8}[/tex] = - 4

Substitute x = - 4 into the equation for corresponding y- coordinate

y = 4(- 4)² + 32(- 4) - 11

  = 4(16) - 128 - 11

  = 64 - 139

   = - 75

vertex = (- 4, - 75 )

Answer:

9000 Pounds (lbs) = 4.017859 Tons (t)

1 lbs = 0.000446 t

1 t = 2,240 lbs

Step-by-step explanation:

Answer:

Step-by-step explanation:

Lucy=65

Eva= X points

Total:

Points =  65 + 65 = 130

Answer:

[tex]a^{12}[/tex]

Step-by-step explanation:

Identity Used :   [tex]a^x \times a^y = a^{x+ y}[/tex]

       [tex]a^5 \times a^7 = a^{5 + 7} = a^{12}[/tex]

[tex] \frac{dx}{dt} = 28.2 \: \frac{m}{hr}[/tex]

Step-by-step explanation:

Let y = height of the pole = 35 m (constant)

x = length of the shadow

They are related as

[tex] \tan \theta = \frac{y}{x} [/tex]

or

[tex]x = \frac{y}{ \tan\theta } = y \cot \theta[/tex]

Taking the time derivative of the above expression and keeping in mind that y is constant, we get

[tex] \frac{dx}{dt} = y( - \csc^{2} \theta) \frac{d \theta}{dt} [/tex]

Before we plug in the numbers, let's convert the degree unit into radians:

[tex]40° \times ( \frac{\pi \: rad}{180°}) = \frac{2\pi}{9} \: radians[/tex]

Since the angle is decreasing, then d(theta)/dt is negative. Therefore, the rate at which the shadow is lengthening is

[tex] \frac{dx}{dt} = (35 \: m)( - \csc^{2} \frac{2\pi}{9} )( - \frac{1}{3} \frac{rad}{hr} )[/tex]

or

[tex] \frac{dx}{dt} = 28.2 \: \frac{m}{hr} [/tex]

The line the puck traveled is the hypotenuse of a right triangle.

Using the Pythagorean theorem:

Travel = sqrt( 4^2 + 30^2)

Travel = sqrt( 16 + 900)

Travel = sqrt(916)

Travel = 30.265 feet ( round the answer as needed)

Step-by-step explanation:   6  22  22  51

one orange box is 10  the other box looks like 15

the scale factor is 15/10  or 1.5

the smaller triangle blue box is a 4

multiply 4 by the scale factor  1.5

  4 × 1.5  = 6

Answer:

(a) [tex]y = 350,000 \times (1 + 0.07132)^t[/tex]

(b) (i) The population after 8 hours is 607,325

(ii) The population after 24 hours is 1,828,643

(c) The rate of increase of the population as a percentage per hour is 7.132%

(d) The doubling time of the population is approximately, 10.06 hours

Step-by-step explanation:

(a) The initial population of the bacteria, y₁ = a = 350,000

The time the colony grows, t = 12 hours

The final population of bacteria in the colony, y₂ = 800,000

The exponential growth model, can be written as follows;

[tex]y = a \cdot (1 + r)^t[/tex]

Plugging in the values, we get;

[tex]800,000 = 350,000 \times (1 + r)^{12}[/tex]

Therefore;

(1 + r)¹² = 800,000/350,000 = 16/7

12·㏑(1 + r) = ㏑(16/7)

㏑(1 + r) = (㏑(16/7))/12

r = e^((㏑(16/7))/12) - 1 ≈ 0.07132

The  model is therefore;

[tex]y = 350,000 \times (1 + 0.07132)^t[/tex]

(b) (i) The population after 8 hours is given as follows;

y = 350,000 × (1 + 0.07132)⁸ ≈ 607,325.82

By rounding down, we have;

The population after 8 hours, y = 607,325

(ii) The population after 24 hours is given as follows;

y = 350,000 × (1 + 0.07132)²⁴ ≈ 1,828,643.92571

By rounding down, we have;

The population after 24 hours, y = 1,828,643

(c) The rate of increase of the population as a percentage per hour =  r × 100

∴   The rate of increase of the population as a percentage = 0.07132 × 100 = 7.132%

(d) The doubling time of the population is the time it takes the population to double, which is given as follows;

Initial population = y

Final population = 2·y

The doubling time of the population is therefore;

[tex]2 \cdot y = y \times (1 + 0.07132)^t[/tex]

Therefore, we have;

2·y/y =2 = [tex](1 + 0.07132)^t[/tex]

t = ln2/(ln(1 + 0.07132)) ≈ 10.06

The doubling time of the population is approximately, 10.06 hours.